Accuracy, Units, Form
We have seen how tasks define what problems students have to solve. However, students often have to do extra work after solving the task. Examples are:
- Numerically evaluating and possibly rounding the result
- Writing the result with the proper unit.
- Writing the result in scientific notation.
You can configure these settings using the Accuracy, Units and Form toggles at the bottom of a multistep task.
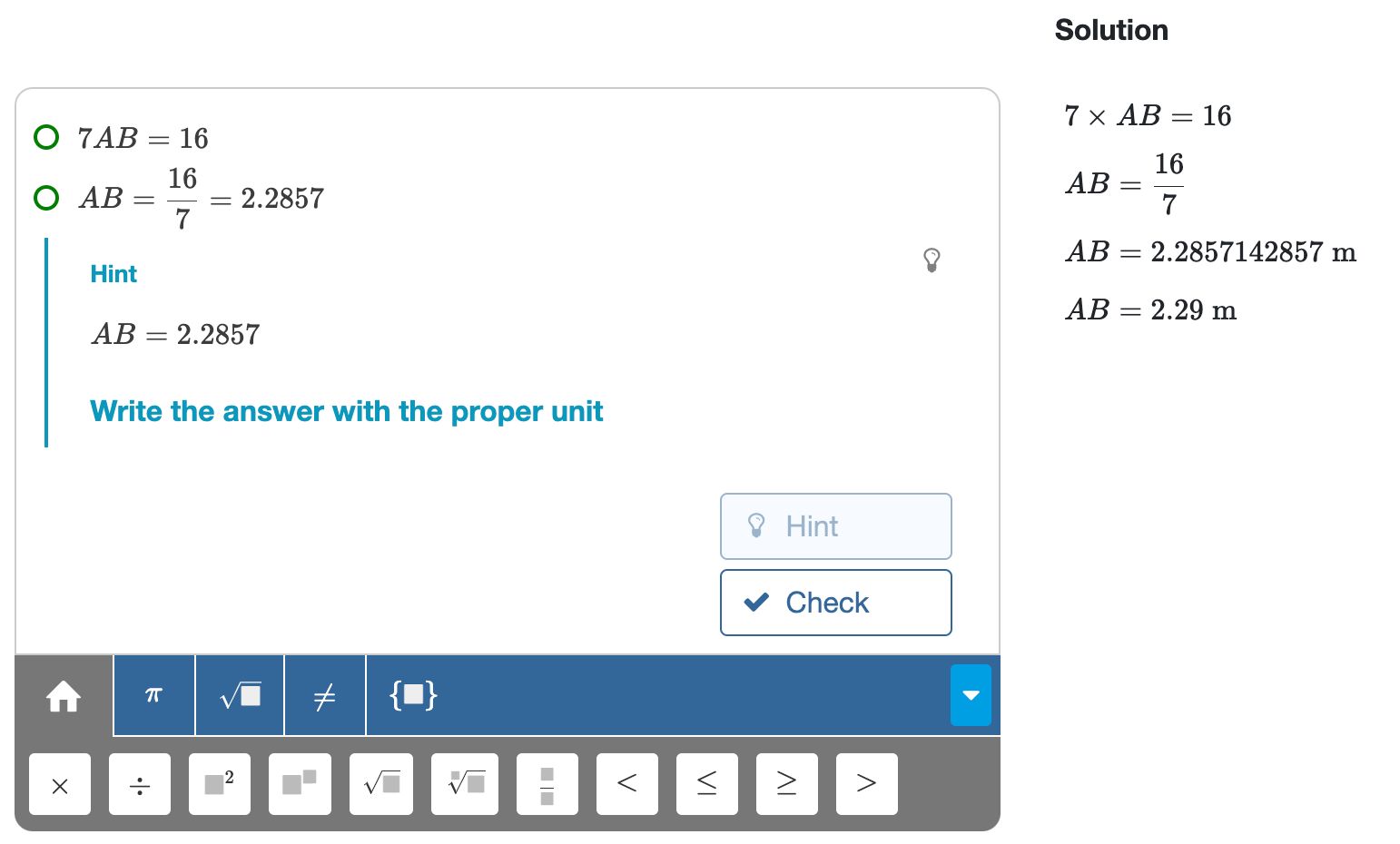
Accuracy settings
Click on the accuracy option to reveal its settings.
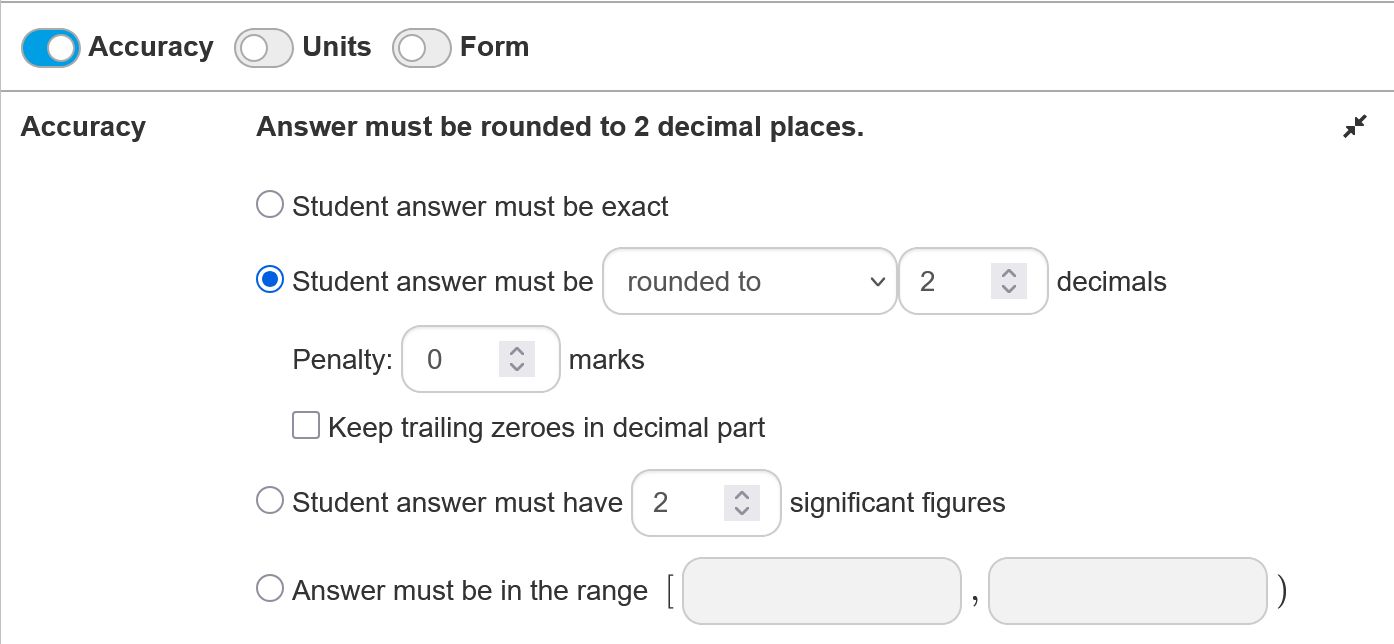
The default setting is 'exact', meaning students should not approximate their answers. So students should keep roots and fractions if these cannot be written in an exact decimal form.
- The exact solution of is or , but not .
- The exact solution of is , , or .
Any other option than 'exact' implies that students must numerically approximate the result. We will discuss the various types of approximations below.
Rounded to .. decimals
Students must round the answer to the prescribed number of decimal places.
Example: Round to two decimals
- intermediate step. Too many decimal places.
- incorrect. Not enough decimal places.
- incorrectly rounded.
- final answer
Accurate to ... decimals
The answer must be accurate to at least the prescribed number of decimals.
Example: Write accurate to two decimals
- final answer
- final answer
- incorrect, not accurate enough.
Significant figures
Significant figures are the number of digits in a value. For example, 3.1415 has five signification figures. This type of accuracy is expected in STEM problems where calculations usually depend on measured values.
Example: Approximate to three significant figures
- intermediate step. Not enough significant figures.
- intermediate step. Too many significant figures.
- final answer.
Range
Sometimes you want to set the upper and lower bounds explicitly. An example is a length which students must measure with their ruler. Note that the range always includes the lower bound but excludes the upper bound.
Units
You can use Multistep for calculations that involve quantities and units. Algebrakit recognizes the notations of many standard units and can convert one unit into another.
Just like rounding, adding the unit is something you usually do at the end of a derivation. This way of working, and some other settings, can be configured in the Unit Settings.
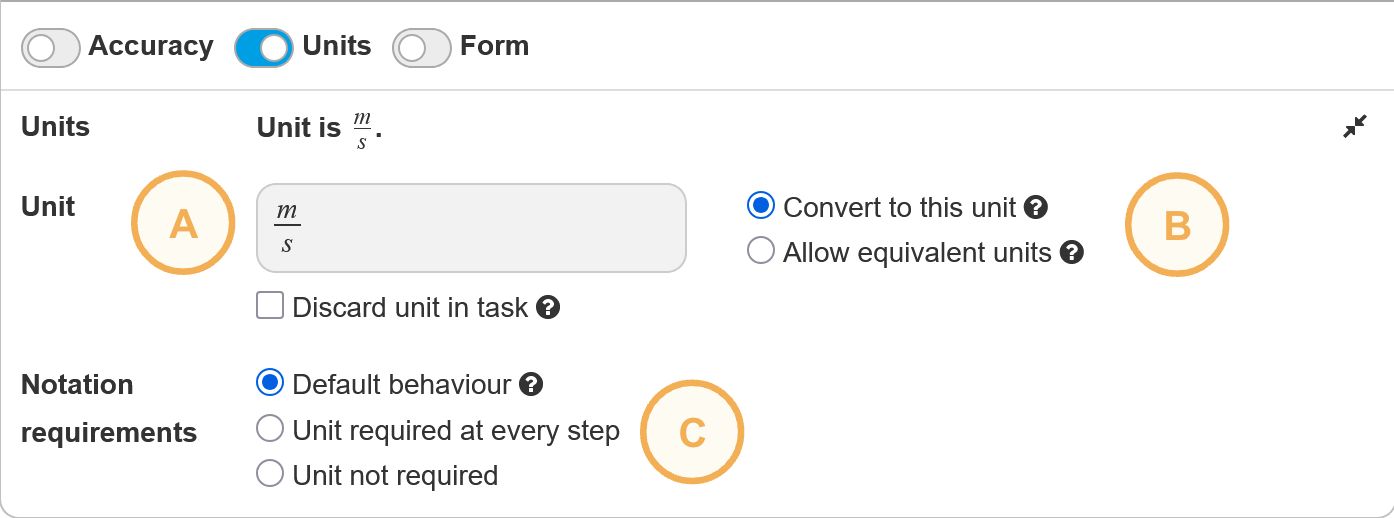
The elements in the Unit Settings are divided into three categories, as indicated by the yellow labels in the image.
- (A) The unit of the result. If also the task has a unit, then it will be converted. Otherwise, it will be added. See the figure below.
- (B) Whether equivalent units are allowed as a final answer or if students need to convert these to the desired unit.
- (C) Is the unit optional or required? Is it allowed to postpone adding the unit toward the end of the derivation (which is the default behavior), or must it be written with every intermediate step?

Form
In the Form menu you can configure properties of the form of the final answer. For example, the worked solution to a STEM question should be in scientific notation. Or, you may require students to give their final answer as a mixed fraction rather than an improper fraction.
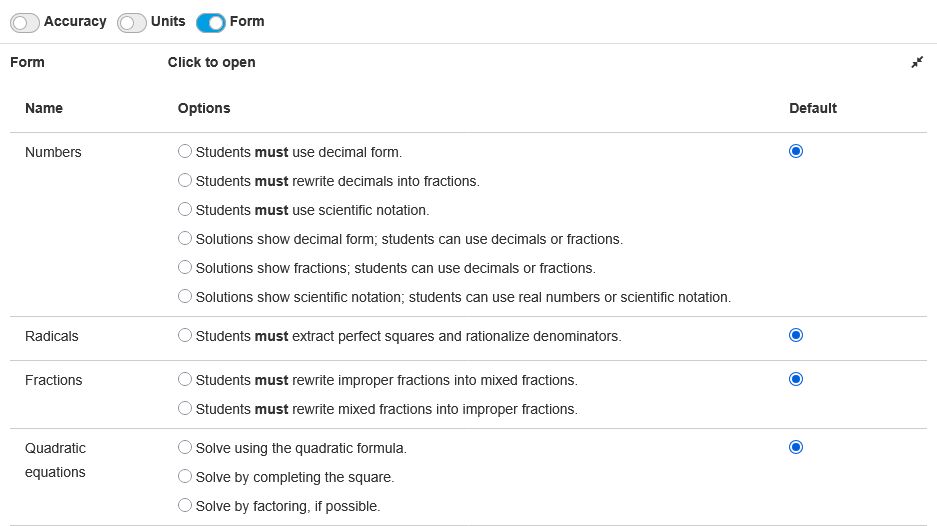
The Form menu has three settings to configure different properties of a final answer.
- The Numbers setting defines number notation, such as decimal, fraction, or scientific notation.
- The Radicals setting defines notation requirements for roots.
- The Fractions setting defines what fraction types are allowed, such as improper or mixed fractions
If you do not choose an option, Algebrakit will use the default settings from the student profile.
Numbers
The Numbers setting determines accepted notations for student answers. You can enforce decimal, fractional, and scientific notation. You can also choose the preferred notation in worked solutions.
The default setting allows both fractions and decimal notation. For example, a student can answer if the expected answer is .
If you require students to write their final answer in a specific form, Algebrakit will still accept any notation as intermediate steps.
The setting "Students must rewrite decimals into fractions." does not require students to write their fractions in any particular form. If you want to require students to write their final answers either as improper or mixed fractions, adjust the Fractions setting.
Radicals
The Radicals setting has only two options. The default option follows the student profile. The option "Students must extract perfect squares and rationalize denominators" requires students to normalise radicals. For example, students must rewrite into and into .
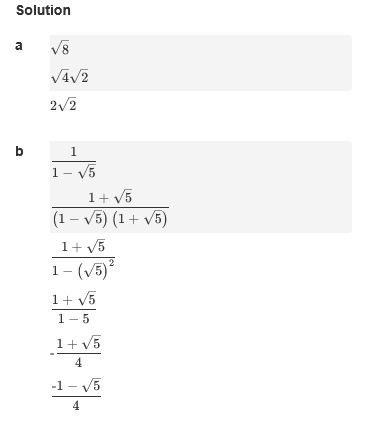
Fractions
You can require students to write fractions as improper fractions or as mixed fractions.
This setting does not require students to write their answers as fractions. Unless you change the Numbers setting to require students to rewrite decimals into fractions, students may write their answer in decimal notation.
